Background
The Diffie-Hellman key exchange protocol is an incredibly important and common algorithm in cryptography and digital communications. The key exchange is used by two parties to generate a shared private key through a public domain. In brief, two parties, Alice and Bob, choose a very large prime number p and a non-zero integer g, both of which are in the public domain. Both Alice and Bob then choose secret integer numbers that only they know, a for Alice and b for Bob.
Alice then computes A = (g^a)(mod p), while Bob computes B = (g^b)(mod p).
Alice and Bob then exchange their results through the public domain and use them to compute a shared secret key.
Alice: Secret key = (B^a)(mod p) = (g^(b*a))(mod p)
Bob: Secret key = (A^b)(mod p) = (g^(a*b))(mod p)
In principle, the numbers used in these key exchanges are very large and its computationally futile to try and figure out the secret key if you are an attacker with access only to the public domain.
Challenge
Diffie-Hellman key exchangers require a lot of multiplication procedures to be carried out by processors. As such in this simulated world a hardware multiplier would help reduce the load on the computing systems. The program for a Diffie-Hellman key exchange was given. My task was to analyze the multiplication code and turn it into a simulated hardware multiplier in SystemC. The hardware multiplier had to be able to communicate with the Diffie-Hellman key exchanger via a handshaking protocol.
Handshaking
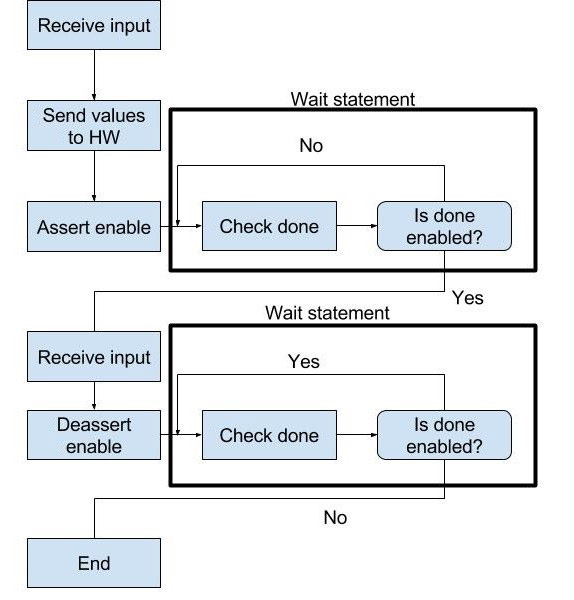
As provided, the code interfaced the hardware that had yet to be developed and the software with a few timed waits. A more robust link between software and hardware was required and implemented with a two signal system.
- Once the software received two 32-bit numbers that needed to be multiplied, an enable signal was asserted and the numbers transmitted.
- When the hardware finished the multiplication, the product was returned to the software and the done signal was pulled high.
- The software received the product and de-asserted the enable signal.
- The hardware then de-asserted the done signal, ending the handshaking and multiplication processes.
During the handshaking and multiplication processes the software and hardware were represented with state machines. Shown below on the left is the state machine for the software, while on the right is the state machine for the hardware.
- The software was based around wait statements, that occurred while the multiplication and handshaking process was taking place.
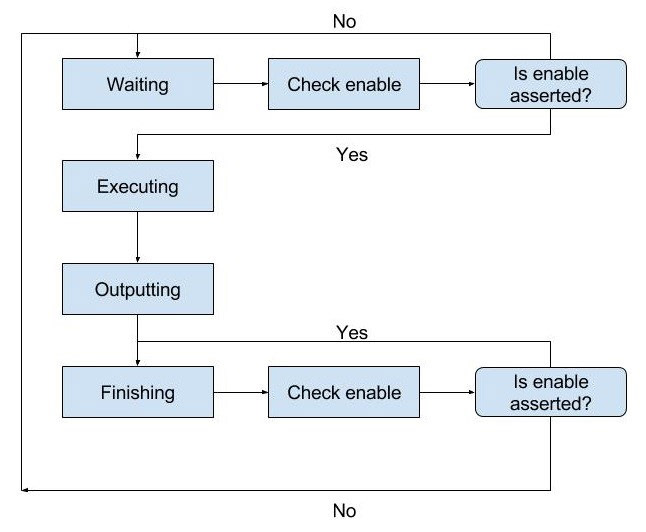
Hardware Multiplier
The multiplication process was broken down into the 12 following steps.
1) Split the inputs into 4 low and high half words (16 bits each).
2) Multiply bLow with cLow to make the low 32 bit word a0.
3) Multiply bLow with cHigh to make t (also 32 bits).
4) Multiply bHigh with cLow to make u (also 32 bits).
5) Multiply bHigh with cHigh to make a1 (also 32 bits).
6) t and u are then summed.
7) The sum of t and u is compared with the original value of u (the first if statement).
8) If the sum is lower an overflow occurred, so add 1 to the high half of a1 (1 is shifted 16 bits to the left before the addition).
9) The sum of t and u is shifted into a high half word and assigned to u.
10) a0 is added with the new value of u and compared to the value of the sum of t and u shifted to the left 16 bits.
11) Once again if the new sum of a0 and u is smaller than the old one an overflow has happened and 1 must be added to a1; however this time 1 is added to the lower half so no shifting is required.
12) The final step is to shift the sum of the original t and u 16 bits to the right and to sum it with a1.